2.4 Rings taxonomy

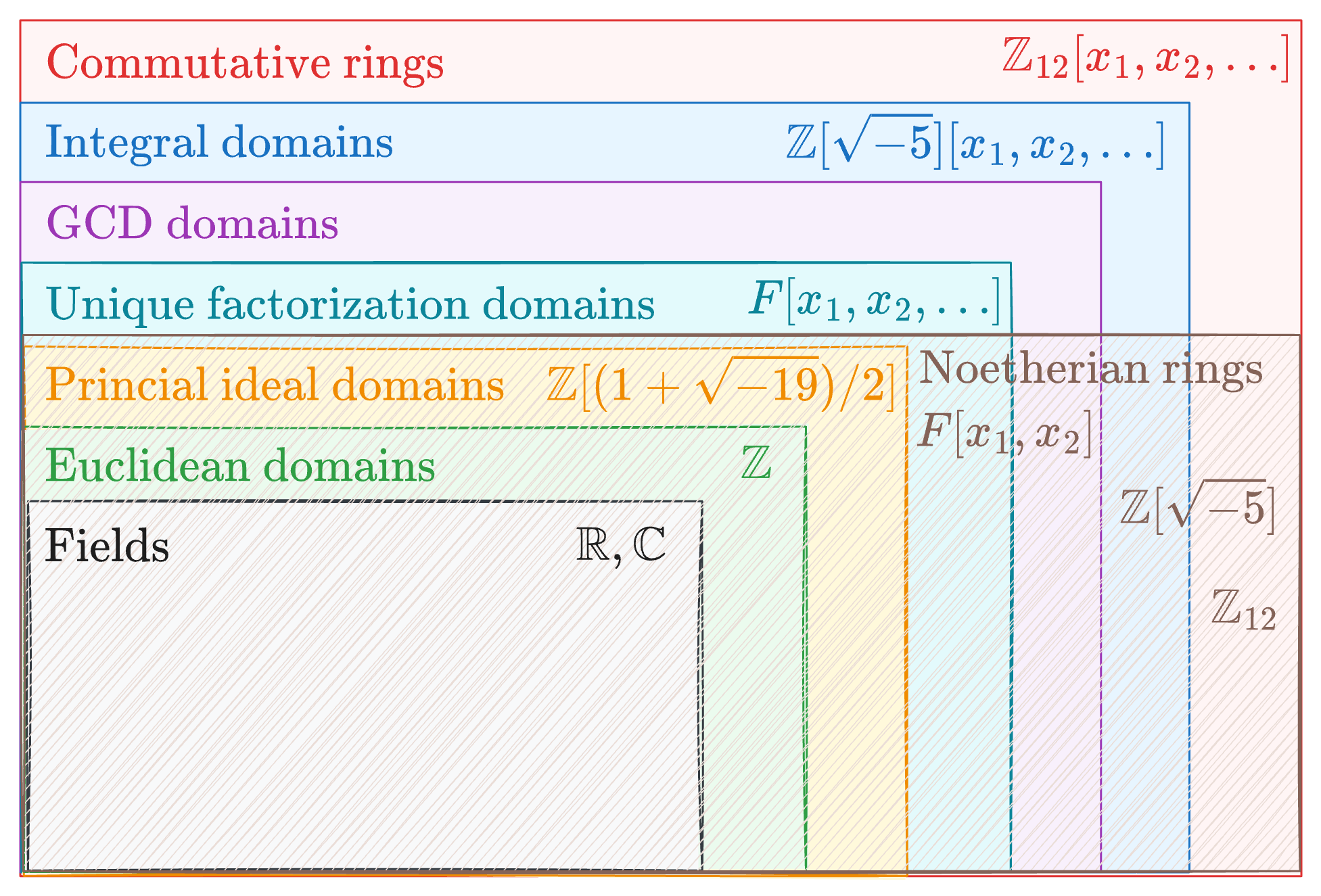
Rings can have different structures and properties because they use two operations: addition and multiplication. The diagram below shows different kinds of rings and how they fit together. We're going to look at and define a few of these types of rings, that will be useful in our discussions.

Commutative rings

def: Commutative ring

$$\begin{align*} &\sphericalangle \\ &A \in \mathcal R^1 \\ &\forall x, y \in A: x\cdot y = y \cdot x \\ \hline \\ &A \in \mathcal R^{\mathcal C} \,\,\, (A \text { is an commutative ring}) \end{align*}$$

note

Here we assume that commutative ring necessary has an identity. Some textbooks don't assume that and some do.

Example 3: Commutative ring

A ring $\Z$ is an example of Commutative ring.

Example 4: Non-commutative ring

A ring of 2x2 matrices over real numbers under matrix $+$ and $\cdot$ is a ring but it's not commutative.

def: a divides b

$$\begin{align*} &\sphericalangle \\ &A \in \mathcal R^{\mathcal C} \\ &a, b \in A, \exists c \in A: b = ac\\ \hline \\ &a \mid b \,\,\,(a\text{ divides } b) \end{align*}$$

def: Prime element

$$\begin{align*} &\sphericalangle \\ &A \in \mathcal R^{\mathcal C} \\ &p \in A \setminus \{0\}: (p\mid ab \implies (p\mid a) \vee(p\mid b)) \\ \hline \\ &r \in \mathfrak P(A)\,\,\, (r \text{ is a prime in } A) \end{align*}$$

Proposition 2.4.1 Prime element and Prime ideal

$$\begin{align*} &\sphericalangle \\ &A \in \mathcal R^{\mathcal C} \\ &p \in A \\ \hline \\ &p \in \mathfrak P(A) \iff \lang p \rang_I \in \mathfrak P_I(A) \end{align*}$$

Proof

$$p \in \mathfrak P(A) \iff (p \mid ab \implies (p \mid a) \vee (p \mid b) ) \iff \\ (\exists z \in A: ab = pz \implies (\exists x \in A: p=ax) \vee (\exists y \in A: p=by)) \iff \\ (ab \in \lang p \rang_I \implies (a \in \lang p \rang_I)\vee(b \in \lang p \rang_I))$$

$\square$

Proposition 2.4.2 Finitely generated ideal explicit form

$$\begin{align*} &\sphericalangle \\ &R \in \mathcal R^{\mathcal C} \\ &S \subseteq R, S = \{a_1, \ldots, a_k\} \\ \hline \\ &\lang S \rang_I =\{r_1a_1+\ldots+r_ka_k, r_i \in R\} \end{align*}$$

Proof

Denote $I=\{r_1a_1+\ldots+r_ka_k, r_i \in R\}$. First, let's prove that $I \subseteq_R R:$

$$I \ne \empty \\ \forall s_1, s_2 \in I: s_1 - s_2 = r_{1,1}a_1+\ldots+r_{k, 1}a_k - r_{2, 1}a_1-\ldots-r_{2, k}a_k = \\ =r_{3, 1}a_1+\ldots+r_{3, k}a_k \in I \\ \forall r \in R, s \in I:rs=rr_1a_1+\ldots+rr_ka_k \in I$$

By $(2.3.3)$: $I \subseteq_R R$. Note that the last equation additionally proves that $rI \subseteq I$. The fact that $R \in \mathcal R^{\mathcal C}$ implies $I r \subseteq I$ as well. Thus, $I \lhd_R R$.

Finally it's obvious that $S \subseteq I$ and any ideal containing $S$ must at least contain $I$ ($r_ia_i$ must be in this ideal and thus their sums as well).

$\square$

Integral domains

def: Integral domain

$$\begin{align*} &\sphericalangle \\ &B \in \mathcal R^{\mathcal C} \\ &\forall x, y \in B \setminus \{0\}: x\cdot y \ne 0 \\ \hline \\ &B \in \mathcal R^{\mathcal{ID}} \,\,\, (B \text { is an integral domain}) \end{align*}$$

Example 5: Integral domain

A ring $\Z$ is obviously an intergral domain, since there are no integers in $\Z \setminus \{0\}$ that can have a $0$ product.

Example 6: Non-integral domain

$\Z_6 \in \mathcal R^{\mathcal C}, \Z_6 \notin \mathcal R^{\mathcal{ID}}$ since $2 \cdot 3 = 0 \pmod 6$.

Proposition 2.4.3 Cancellation law

$$\begin{align*} &\sphericalangle \\ &B \in \mathcal R^{\mathcal{ID}} \\ \hline \\ &\forall a, b, c\in B: ab=ac \implies (a=0) \vee(b=c) \end{align*}$$

Proof

$$ab=ac \implies a(b-c)=0 \implies (a=0)\vee(b-c=0)$$

$\square$

Proposition 2.4.4 Finite integral domain is a field

$$\begin{align*} &\sphericalangle \\ &B \in \mathcal R^{\mathcal{ID}} \\ &|B| < \infty \\ \hline \\ &\forall a \in B \setminus \{0\}: \exists b \in B: ab = 1 \end{align*}$$

Proof

$$\forall a \in B \setminus \{0\}, f: B \to B, x \mapsto ax \overset{(2.4.3)}{\implies} f: B\overset{1-1}{\to} B \implies \\ |B|=|f(B)| \overset{f(B) \subseteq B}{\implies}\\ B = f(B) \implies f: B \leftrightarrow B \implies \exists b \in B: ab = 1$$

$\square$

Proposition 2.4.5 Characteristic is prime or 0

$$\begin{align*} &\sphericalangle \\ &B \in \mathcal R^{\mathcal ID} \\ \hline \\ &(\text{char }B=0)\vee(\text{char }B \in \mathfrak P) \end{align*}$$

Proof

$$\text{char } B > 0, \text{char } B \notin \mathfrak P \implies \\ \text{char } B = n = ab, 1 < a, b < n \implies \\ 0=n\cdot1 = (a\cdot 1)(b\cdot 1) \overset{B \in \mathcal R^{\mathcal ID}}\implies \\(a\cdot 1 = 0) \vee (b\cdot 1 = 0) \overset{(2.3.2)}\implies \text{char } B < n$$

Thus, $(\text{char }B=0)\vee(\text{char }B \in \mathfrak P)$

$\square$

def: Unit

$$\begin{align*} &\sphericalangle \\ &R \in \mathcal R^1 \\ &u \in R: \exists v \in R: u \cdot v=v \cdot u=1 \\ \hline \\ &u \in R^* \,\,\,(u\text{ is a unit}) \end{align*}$$

def: Irreducible element

$$\begin{align*} &\sphericalangle \\ &B \in \mathcal R^{\mathcal {ID}} \\ &r \in B \setminus (B^* \cup \{0\}), (r = uv \implies (u \in B^*) \vee(v \in B^*)) \\ \hline \\ &r \in B^{-} \,\,\, (r \text{ is an irreducible element of } B) \end{align*}$$

def: Reducible element

$$\begin{align*} &\sphericalangle \\ &B \in \mathcal R^{\mathcal {ID}} \\ &r, s, t \in B \setminus (B^* \cup \{0\}): r = st \\ \hline \\ &r \in B^+ - \text{reducible} \end{align*}$$

note

Any element of integral domain is either 0, unit, reducible or irreducible. Thus $B = \{0\} \cup B^* \cup B^+ \cup B^-$ and all sets are disjoint.

In theory we could define units, reducible and irreducible elements for commutative rings, however in this case we won't have this neat property as commutative ring can have zero divisors.

note

The other way to think about reducible and irreducible is as follows: consider a subset of non-zero, non-invertible elements of $B$. Each element in this set either a product of two elements from itself (reducible) or not (irreducible)

Proposition 2.4.6 Units, divisibility and ideals

$$\begin{align*} &\sphericalangle \\ &B \in \mathcal R^{\mathcal{ID}} \\ &a, b \in B \setminus \{0\} \\ &I \lhd_R B \\ \hline \\ &\begin{align*} & a \mid b \iff \lang b \rang_I \subseteq \lang a \rang_I \tag{a}\\ & \exists u \in B^*: b = au \iff \lang a \rang_I = \lang b \rang_I \hspace{1cm} \tag{b}\\ & B^* \cap I \ne \empty \iff I = B \tag{c}\\ \end{align*} \end{align*}$$

Proof

a.

$\implies$

$$a \mid b \implies \exists c \in B: b = ac \implies \\\forall x \in \lang b \rang_I: \exists r \in B: x = rb=rac=rca \in \lang a \rang_I \\$$

$\impliedby$

$$\lang b \rang_I \subseteq \lang a \rang_I \implies b \in \lang a \rang_I \implies \exists r \in B: b = ra \implies a \mid b$$

b.

$\implies$

$$\exists u \in B^*: b = au \overset{(a)}\implies \lang b \rang_I \subseteq \lang a \rang_I \\ a = bu^{-1} \overset{(a)}{\implies} \lang a \rang_I \subseteq \lang b \rang_I$$

$\impliedby$

$$\lang b \rang_I = \lang a \rang_I \overset{(a)}{\implies} a \mid b, b \mid a \implies \exists x, y \in B: a = bx, b = ay = bxy \implies \\ xy=1 \implies \exists u=y \in B^*, b = au$$

c.

$\implies$

$$a \in B^* \cap I \implies aa^{-1} \in I \implies 1 \in I \implies \\ \forall r \in R: r = r\cdot 1 \subseteq I \implies R = I$$

$\impliedby$

$$R = I \implies 1 \in B^* \cap I \implies B^* \cap I \ne \empty$$

$\square$

note

The $(d)$ property holds for the rings with identity in general, not just for the integral domains.

Proposition 2.4.7 Prime is irreducible

$$\begin{align*} &\sphericalangle \\ &B \in \mathcal R^{\mathcal {ID}} \\ &p \in \mathfrak P(B) \\ \hline \\ &p \in B^- \end{align*}$$

Proof

$$p \in \mathfrak P(B) \overset{(2.4.1)}{\implies} \lang p \rang_I \in \mathfrak P_I(B) \\ p = ab \implies ab \in \lang p \rang_I \implies (a \in \lang p \rang_I) \vee (b \in\lang p \rang_I) \\ \begin{cases} a \in \lang p \rang_I \implies \exists r \in B:p = ab=prb \overset{(2.4.3)}{\implies} rb = 1 \implies b \in B^* \\ b \in \lang p \rang_I \implies \exists r \in B:p = ab=arp \overset{(2.4.3)}{\implies} ar = 1 \implies a \in B^* \end{cases}$$

$\square$

Proposition 2.4.8 Factor ring by prime ideal is an integral domain

$$\begin{align*} &\sphericalangle \\ &R \in \mathcal R^{\mathcal C} \\ &I \lhd_R R \\ \hline \\ &I \in \mathfrak P_I \iff R/I \in \mathcal R^{\mathcal{ID}} \end{align*}$$

Proof

$\implies$

$$\forall a + I, b + I \in R/I: (a+I)(b+I)=I \implies ab+I=I \implies \\ ab \in I \overset{I \in \mathfrak P_I}{\implies} (a \in I) \vee (b \in I) \implies (a+I = I) \vee(b+I = I)$$

$\impliedby$

$$\forall a, b \in R:ab \in I \implies I= ab+I = (a+I)(b+I) \overset{ R/I \in \mathcal R^{\mathcal{ID}}}{\implies} \\ (a+I=I)\vee(b+I=I) \implies (a \in I)\vee(b \in I)$$

$\square$

Noetherian rings

def: Noetherian ring

$$\begin{align*} &\sphericalangle \\ &N \in \mathcal R^{\mathcal {C}} \\ &\forall J_i \lhd_I N: J_1 \subseteq J_2 \subseteq \ldots: \exists n_0: \forall n \ge n_0: J_n=J_{n_0} \\ \hline \\ &N \in \mathcal R^{\mathcal {N}} \,\,\, (R \text{ is a noetherian ring}) \end{align*}$$

Proposition 2.4.9 Ideals are finitely generated

$N \in \mathcal R^{\mathcal {N}} \iff \forall I \lhd_I N: \exists S \subseteq N, |S| < \infty: I = \lang S \rang_I$

Proof

$\implies$

Consider $I \lhd_R N$ and $X:= \{J \lhd_R I, J=\lang j_1, \ldots, j_k\rang_R\}$ - the set of all finitely generated ideals contained in $I$. We want to prove that $I \in X$, so it's finitely generated.

Obviously, $X \ne \empty$.

Assume $\forall J \in X: \exists K \in X: K \supset J$. That would imply that we can take and ideal $J_1$, then $J_2:=K \supset J_1$, then $J_3:=K \supset J_2$, so we build a sequence $J_1 \subset J_2 \subset J_3 \subset \ldots$ which never stabilizes and contradicts $N \in \mathcal R^{\mathcal {N}}$. So we have

$$\exists J \in X: \forall K \in X: K \subseteq J$$

Assume $J \ne I$. Since $J \in X$, by definition of $X$ we have $J \subseteq I$. So $J \subset I$ and $\exists a \in I \setminus J$. Consider an ideal $L:=\lang a \rang_I+J$. $L$ is finitely generated and $L \subseteq I$, so $L \in X$. On the other hand $L \supset J$. But this is a contradiction to the definition of $J$. Thus, $J=I$ and so $I$ is finitely generated.

$\impliedby$

Consider $J_1 \subseteq J_2 \subseteq \ldots$ and $J:=\cup_iJ_i$. Let's prove that $J$ is ideal:

$$J \ne \empty \\ a, b \in J \implies a \in J_i, b \in J_k \implies \\ ((a - b) \in J_i)\vee((a - b) \in J_k) \implies a-b \in J \\ r \in N, a \in J \implies a \in J_i, ra \in J_i \implies ra \in J.$$

Since by our assumption every ideal is finitely generated, $J=\lang a_1, \ldots, a_k\rang_I$. If $a_i \in J_{n_i}$, define $n:=\max_{1\le i \le k}n_i$. Then $\forall i: 1 \le i \le k: a_i \in J_n$. This immediately implies $J_n\supseteq J$. So we have $\forall k \ge n: J\subseteq J_n \subseteq J_k \subseteq J$, or $J_k=J_n$.

$\square$

GCD domain

def: Greatest common divisor

$$\begin{align*} &\sphericalangle \\ &R \in \mathcal R^{\mathcal {ID}} \\ &a, b, d \in R \\ &d \in R: d \mid a, d \mid b \\ &\forall d_1 \in R: d_1\mid a, d_1\mid b \implies d\mid d_1 \\ \hline \\ &\gcd(a,b):=d \end{align*}$$

def: GCD domain

$$\begin{align*} &\sphericalangle \\ &D \in \mathcal R^{\mathcal {ID}} \\ &\forall a, b \in D: \exists \gcd(a, b)\\ \hline \\ &D \in \mathcal R^{\mathcal {GCD}} \end{align*}$$

Proposition 2.4.10: Divisibility is specified up to a unit

$$\begin{align*} &\sphericalangle \\ &A \in \mathcal R^{\mathcal C} \\ & a, b \in R \\ & u \in R^* \\ \hline \\ &a \mid b \iff ua \mid b \iff a \mid ub \iff ua\mid ub \end{align*}$$

Proof

$$a\mid b \implies b = ca=(cu^{-1})ua \implies ua \mid b \\ ua\mid b \implies b=cua \implies ub=(ucu)a \implies a \mid ub \\ a\mid ub \implies ub=ca=(cu^{-1})ua \implies ua \mid ub \\ ua \mid ub \implies ub = cua \implies b = (u^{-1}cu)a \implies a \mid b$$

$\square$

Proposition 2.4.11: GCD is unique up to a unit multiple

$$\begin{align*} &\sphericalangle \\ &D \in \mathcal R^{\mathcal {GCD}} \\ &a, b, d_1, d_2 \in D \\ &d_1 \ne d_2 \\ &d_1 = \gcd(a, b) \\ &d_2 = \gcd(a, b) \\ \hline \\ &\exists u \in D^*: d_1 = ud_2 \end{align*}$$

Proof

$$d_1 \mid d_2 \implies \exists x \in D: d_2 = xd_1 \\ d_2 \mid d_1 \implies \exists u \in D: d_1 = ud_2 \\ d_1 = ud_2=uxd_1 \implies 1 = ux \implies u \in D^*$$

$\square$

Example: GCD Domain

An example of a GCD domain is the ring of integers $\Z$. In $\Z$, the gcd of any two integers exists and is unique up to sign, which is a special case reflecting the more general property in GCD domains where gcds are unique up to units.

Example: Non-GCD Domain

$\Z[\sqrt{-5}]$ (a minimal ring containing $\Z$ and $\sqrt{-5}$) is an example of non-gcd domain. We will not prove this, but the proof can be found here.

Unique factorization domains

def: Unique factorization domain

$$\begin{align*} &\sphericalangle \\ &U \in R^{\mathcal{ID}} \\ 1.\,\,\, &\forall x \in (U \setminus (U^* \cup \{0\}) ): \exists a_1,\ldots,a_n \in U^{-}:x= a_1 \cdot\ldots \cdot a_k \\ 2.\,\,\, & \forall a_1,\ldots,a_k,b_1,\ldots,b_n \in U^- : a_1 \cdot\ldots \cdot a_k=b_1 \cdot\ldots \cdot b_n \implies \\ &n=k, \exists \sigma \in S_n, u_1, \ldots, u_n \in U^*: \sigma(a_i) = u_ib_i \\ \hline \\ &U \in \mathcal{R}^{\mathcal{UFD}} \,\,\,(U - \text{unique factorization domain} ) \end{align*}$$

A Unique Factorization Domain is basically a type of ring where the Fundamental Theorem of Arithmetic applies. This theorem states that every element in the ring can be broken down into a product of prime elements, and this breakdown is unique except for the order of the factors. In this context, 'prime' elements are referred to as irreducible elements. This is similar to the definition of prime numbers for integers, with the understanding that in the case of integers, the only units (elements that have a multiplicative inverse) are 1 and -1.

Example 7. Unique factorization domain

$\Z$, the ring of integers, is a Unique Factorization Domain (UFD) because the Fundamental Theorem of Arithmetic is valid in this ring.

Example 8. Non-unique factorization domain

$\Z[\sqrt{-5}]:=\{a+b \sqrt{-5}, a, b \in \Z\}$ is an integral domain but not a unique factorization domain. The counter example is $6=2 \cdot 3=(1-\sqrt{-5})\cdot(1+\sqrt{-5})$, where all factors are irreducible.

Proposition 2.4.12: Irreducible = prime

$$\begin{align*} &\sphericalangle \\ &P \in \mathcal R^{\mathcal{UFD}} \\ \hline \\ &p \in P^{-} \iff &p \in \mathfrak P(A) \end{align*}$$

Proof

$\implies$

Consider $a, b \in P: p \mid ab$. Since $P \in \mathcal R^{\mathcal{UFD}}$ we can factor out $a= a_{1}\cdot \ldots \cdot a_{k}\cdot, b= b_{1}\cdot \ldots \cdot b_{n}, a_i, b_i \in P^-$. Then we have:

$$p \mid ab \implies ab = pr \implies a_{1}\cdot \ldots \cdot a_{k}\cdot b_{1}\cdot \ldots \cdot b_{n} = pr$$

Note that on the left-hand side we have irreducibles and on the right-hand side $p$ is irreducible and $r$ is some element. By the property (2) (unique factorization) of UFD, we know that $p$ is some factor on the left-hand side, multiplied by a unit. In other words:

$$(up=a_i) \vee (vp=b_j), u, v \in P^*$$

If $up=a_1$, then $p = a_1u^{-1}$ then $a = u^{-1}\cdot p\cdot a_2 \cdot \ldots \cdot a_k \implies p \mid a$. Similarly $up=a_j \implies p \mid a$, $vp=b_j \implies p \mid b$.

$\impliedby$

Follows from $(2.4.7)$

$\square$

Proposition 2.4.13: UFD is a GCD domain

$$\begin{align*} &\sphericalangle \\ &U \in \mathcal R^{\mathcal {UFD}} \\ \hline \\ &U \in \mathcal R^{\mathcal {GCD}} \end{align*}$$

Proof

Take $a, b \in U$. We can factor $a = up_1^{e_1}\ldots p_n^{e_n}, b = up_1^{f_1}\ldots p_n^{f_n}, p_i \in U^-, e_i, f_i \ge 0$.

Define $d:=p_1^{\min(e_1, f_1)}\ldots p_n^{\min(e_n, f_n)}$. Then it's obvious $d \mid a, d \mid b$.

Consider $c: c \mid a, c \mid b, c = q_1^{g_1}\ldots q_k^{g_k}, q_i \in U^-$.

$$q_i \mid c, c \mid a, c \mid b \implies q_i \mid a, q_i \mid b \overset{p_i, q_i \in \mathfrak P}{\implies} \exists j: q_i = p_j \implies \\ \{q_1, \ldots, q_k\} \subseteq \{p_1, \ldots, p_n\} \\ c \mid a, c \mid b \implies g_i \le \min(e_i, f_i) \implies d \mid c$$

$\square$

Principal ideal domains

def: Principal ideal domains

$$\begin{align*} &\sphericalangle \\ &R \in \mathcal R^{\mathcal{ID}} \\ &\forall I \lhd_R R: \exists a \in R: I=\lang a \rang_I \\ \hline \\ &R \in \mathcal R^{\mathcal {PID}} \,\,\, (R - \text{principal ideal domain}) \end{align*}$$

Example: Principal ideal domain

$\Z$ is a principal ideal domain (PID). It follows from the fact that $\Z$ is an euclidean domain and euclidean domain is a principal ideal domain (the proposition we will prove below)

Example: Non-principal ideal domain

$\Z[x]$ - a unique factorization domain of polynomials with integer coefficients is not a PID. Consider $I = \lang 5, x \rang_I$. Assume that $\exists p \in \Z[x]: I =\lang p \rang_I$. Then $5=p(x)f(x) \implies p(x) = p \in \Z$. Next, $x = pg(x) \implies g(x) = \pm x, p = \mp 1 \implies \lang p(x) \rang_I=\Z[x]$. Thus we can write $3 = 5f(x)+xg(x) \implies g(x) = 0, 3=5f(x)$, but this is impossible for $f(x) \in \Z[x]$.

Proposition 2.4.14: Irreducible element generates maximal ideal

$$\begin{align*} &\sphericalangle \\ &P \in \mathcal R^{\mathcal {PID}} \\ & p \in P \setminus \{0\} \\ \hline \\ &\lang p \rang_I \in \mathfrak M_I(P) \iff p \in P^{-} \end{align*}$$

Proof

$\implies$

We want to prove that $p = uv \implies (u \in P^*)\vee(v \in P^*)$.

$$\lang p \rang_I \in \mathfrak M_I(P), p = uv \overset{(2.4.6)}\implies \lang p \rang_I \subseteq \lang u \rang_I \overset{\lang p \rang_I \in \mathfrak M_I(P)}{\implies} \\ \begin{cases} \lang p \rang_I = \lang u \rang_I \overset{(2.4.6)}\implies \exist x \in P^*: ux = p = uv \implies v = x \in P^*\\ \lang u \rang_I = P \overset{(2.4.6)}\implies u \in P^* \end{cases} \\$$

$\impliedby$

We want to prove that $\forall a \in P: \lang p \rang_I \subseteq \lang a \rang_I \subseteq P \implies (\lang a \rang_I=P)\vee(\lang p \rang_I=\lang a \rang_I)$

$$\forall a \in P: \lang p \rang_I \subseteq \lang a \rang_I \subseteq P \implies \exists x \in P: p = ax \overset{p \in P^-}\implies \\ \begin{cases} x \in P^* \overset{(2.4.6)}\implies \lang p \rang_I = \lang a \rang_I \\ a \in P^* \overset{(2.4.6)}\implies \lang a \rang_I = P \end{cases}$$

$\square$

Proposition 2.4.15: Irreducible = prime

$$\begin{align*} &\sphericalangle \\ &P \in \mathcal R^{\mathcal{PID}} \\ \hline \\ &p \in P^{-} \iff &p \in \mathfrak P(P) \end{align*}$$

Proof

$\implies$

$$(2.4.14) \implies \lang p \rang_I \in\mathfrak M_I(P) \overset{(2.3.6)}{\implies} \lang p \rang_I \in\mathfrak P_I(P) \overset{(2.4.1)}\implies p \in \mathfrak P(P) \\$$

$\impliedby$

Follows from $(2.4.7)$

$\square$

note

We proved in $(2.4.12)$ that irreducible is prime for UFD. Further, we'll see that each PID is a UFD (in $(2.4.17)$), so this proposition $(2.4.15)$ should be a simple corrolary of $(2.4.12)$ and $(2.4.17)$. Hoewever, the proof for $(2.4.17)$ uses $(2.4.15)$ that's why we need two disctinct proofs in $(2.4.12)$ and $(2.4.15)$.

Proposition 2.4.16: PID is Noetherian

$$\begin{align*} &\sphericalangle \\ &P \in \mathcal R^{\mathcal{PID}}\\ \hline \\ &P \in \mathcal R^{\mathcal{N}} \end{align*}$$

Proof

Consider chain of ideals $I_1 \subseteq I_2 \subseteq \ldots$, define $I:=\bigcup_i I_i$. In $(2.4.9)$ we prove that in this case $I \lhd_R P$. So we have

$$P \in \mathcal R^{\mathcal{PID}} \implies \exists a \in P: I = \lang a \rang_I \implies \exists N \in \N: a \in I_N \implies \\ I=\lang a \rang_I \overset{a \in I_N}\subseteq I_N \overset{I=\bigcup_i I_i}\subseteq I \implies I_N = I \implies \\ \forall n \ge N: I=I_N \subseteq I_n \subseteq I \implies I_n = I_N$$

$\square$

Proposition 2.4.17: PID is UFD

$$\begin{align*} &\sphericalangle \\ &P \in \mathcal R^{\mathcal{PID}}\\ \hline \\ &P \in \mathcal R^{\mathcal{UFD}} \end{align*}$$

Proof

Existence of factorization

Let's prove that $\forall p \in P \setminus (P^* \cup \{0\}): \exists p_1, \ldots p_k \in P^-: p= p_1\cdot \ldots \cdot p_k$.

If $p \in P^-$, then we're done. Otherwise, $\exists p_1, p_2 \in P \setminus (P^* \cup \{0\}): a = p_1p_2$. If both of these elements are irreducible, we're done. Otherwise, assime $p_1$ is reducible, that means $p_1=p_{11}p_{12}$ and we can repeat the process until we get $p=p_1\ldots p_k$, where $p_i$ is irreducible.

Now the only question is - why does this process ever terminate? In other words why is $k$ finite? Assume it's not. Then we have infinite sequence $p_1, p_{11}, p_{112}, \ldots$ which we simply denote as $p_1, p_{2}, p_{3}, \ldots$, where $p_{i+1} \mid p_i$. By $(2.4.6)$ and we know that $\lang p_{i} \rang_I \subseteq \lang p_{i+1} \rang_I$. Further note, that not only $p_{i+1} \mid p_i$ but also $p_i = p_{i+1}x$ where $x \notin P^* \cup \{0\}$ (by construction), so by $(2.4.6)$ we cannot have $\lang p_{i} \rang_I = \lang p_{i+1} \rang_I$. So $\lang p_{i} \rang_I \subset \lang p_{i+1} \rang_I$ and we have an ascending chain of ideals $\lang p_{1} \rang_I \subset \lang p_{2} \rang_I \subset \ldots$, that contradicts to the fact that $P$ is Noetherian by $(2.4.16)$.

Uniqueness of factorization

Assume $p_1\ldots p_k=q_1\ldots q_s, p_i, q_i \in P^{-}$. Without the loss of generality $k \le s$.

$$p_1 \in P^{-} \overset{(2.4.15)}{\implies} p_1 \in \mathfrak P(P) \\ p_1 \mid q_1\ldots q_s \implies \exists q_j: q_j = u_1p_1$$

Since $q_j, p_1 \in P^{-}$, we know that $u_1 \in P^*$. Now cancel $p_1$ from both sides, renumerate $q_i$ if necessary to get:

$$p_2\ldots p_k=u_1q_1 \ldots q_{s-1}$$

Making this process $k$ times we get $1 = vq_1\ldots q_{s-k}$. But this means that $q_i \in P^*$, which would contradict to $q_i \in P^-$. So the only way for this equality to hold is $k = s$. And so $p_i =u_iq_j, u_i \in P^*$

$\square$

Euclidean domains

def: Norm

$$\begin{align*} &\sphericalangle \\ &B \in \mathcal R^{\mathcal{ID}} \\ &N: B \to \N \cup 0, N(0) = 0 \\ \hline \\ &N - \text{norm} \end{align*}$$

def: Euclidean domain

$$\begin{align*} &\sphericalangle \\ &E \in \mathcal R^{\mathcal{ID}} \\ &\exists N - \text{norm}: \\ &\forall a, b \in E, b \ne 0: \exists q, r \in E: a = bq + r, (r=0) \vee (N(r) < N(b)) \\ \hline \\ &E \in \mathcal R^{\mathcal E} \end{align*}$$

Example: Euclidean domain

$\Z$ is euclidean domain with $N(x)=|x|$

Proposition 2.4.18 Euclidean domain is PID

$$\begin{align*} &\sphericalangle \\ &E \in \mathcal R^{\mathcal E} \\ \hline \\ &E \in \mathcal R^{\mathcal {PID}} \end{align*}$$

Proof

We'll prove that any ideal is principal. Consider $I \lhd_R E$. If $I = \{0\}$ then we're done. Otherwise assume $d \in I$ is the elemeint with the minimum norm.

Obviously $\lang d \rang_I \subseteq I$. Let's finish the proof by proving $\lang d \rang_I \supseteq I$:

$$\forall a \in I \implies \exists q, r \in E: a = qd + r, (r = 0) \vee (N(r) < N(d)) \\ r = a - qd \implies r \in I$$

By definition of $d: N(r) \ge N(d)$, so by definition of $r$ we can only have $r=0$. So we proved $\forall a \in I \implies a =qd \implies a \in \lang d \rang_I$.

$\square$

Fields

def: Field

$$\begin{align*} &\sphericalangle \\ &F \in \mathcal R^{\mathcal {C}} \\ &F^*= F \setminus \{0\} \\ \hline \\ &F \in \mathcal F \end{align*}$$

Proposition 2.4.19: Field is a euclidean domain

$$\begin{align*} &\sphericalangle \\ &F \in \mathcal F \\ \hline \\ &F \in \mathcal R^{\mathcal {E}} \end{align*}$$

Proof

First, let's prove $F \in \mathcal R^{\mathcal {ID}}$. Consider $a, b \in F^* = F \setminus 0$ and assume $ab=0$. This implies that $a^{-1}ab=0 \implies b=1\cdot b = 0$, which is a contradiction to $b \in F \setminus 0$. So $a \cdot b \ne 0$ and we proved $R \in \mathcal R^{\mathcal {ID}}$.

Next, we define $\forall x \in F: N(x):=0$ and $\forall a, b \in F \setminus \{0\}: a = b\cdot (b^{-1}a)+r$. In this case $r=0$.

$\square$

Proposition 2.4.20: Field criterion

$$\begin{align*} &\sphericalangle \\ &A \in \mathcal R^{\mathcal C} \\ \hline \\ &\text{The following are equivalent:}\\ &\begin{align*} & A \in \mathcal F \tag{a}\\ & I \lhd_R A \implies (I=\{0\})\vee(I=A) \tag{b} \\ & B \in \mathcal R^{\mathcal C} \setminus \{0\}, \phi: A \rightsquigarrow_R B, \phi(1)=1 \implies \ker \phi = \{0\} \hspace{1cm} \tag{c} \end{align*} \\ \end{align*}$$

Proof

$(a) \implies (b)$

Consider an ideal $I\lhd_R A$. It's either zero or has non-zero elements. But in the latter case a non-zero element $a \in F \setminus \{0\}=F^*$, so by $(2.4.6)$ we have $I = A$

$(b) \implies (c)$

$$\phi: A \rightsquigarrow_R B \overset{(2.3.8)}\implies \ker \phi \lhd_RA \overset{(b)}\implies (\ker \phi = \{0\}) \vee(\ker \phi = A) \\ \phi(1)=1 \implies \ker \phi \ne A \implies \ker \phi = \{0\}$$

$(c) \implies (a)$

We will prove that $\forall a \in A \setminus A^*: a = 0$.

$$a \in A \setminus A^* \overset{(2.4.6)}\implies \lang a \rang_I \ne A \implies A / \lang a \rang_I \ne \{0+A\}\\$$

That means if we assume $B:=A / \lang a \rang_I$ and $\phi$ to be natural homomorphism that is $\phi: A \rightsquigarrow_R A / \lang a \rang_I, x \mapsto x+\lang a \rang_I, \phi(1) = 1 + \lang a \rang_I$, then by $(c)$ $\ker \phi = \{0\}$. On the other hand $\ker\psi = \lang a \rang_I$, so $a = 0$.

$\square$

Proposition 2.4.21: Factor ring by maximal ideal is a field

$$\begin{align*} &\sphericalangle \\ &R \in \mathcal R^{\mathcal C} \\ &I \lhd_R R \\ \hline \\ &I \in \mathfrak M_I(R) \iff R/I \in \mathcal F \end{align*}$$

Proof

$\implies$

First, $R \in \mathcal R^{\mathcal C} \overset{(a+I)(b+I)=ab+I}\implies R/I \in \mathcal R^{\mathcal C}$.

Fix some $a+I \in R/I, a \notin I$. We want to prove that it has an inverse.

Consider an ideal $J:=\lang a \rang_I + I$ (it's an ideal by $(2.3.4)$). $a \notin I \implies I \subset J$. Since $I \in \mathfrak M_I(R)$, this means that $J=R$.

$$J=R \implies 1\in J \implies \exists b \in R, i \in I: 1=ba+i \implies \\ 1+I = ba+I=(b+I)(a+I) = (a+I)(b+I) \implies \\ b+I = (a+I)^{-1}$$

$\impliedby$

$R/I \in \mathcal F \implies 0+I, 1+I \in R/I, 0+I \ne 1+I \implies I \subset R$

Fix some $J \lhd_R R, I \subset J$, we want to prove $J=R$. That will imply that $I \in \mathfrak M_I(R)$.

Take some $a \in J \setminus I$ and take some $b \in R: (b+I)=(a+I)^{-1}$. Then

$$ab+I = (a+I)(b+I)=1+I \implies \\ \exists i \in I: ab+i = 1$$

Now note that $a \in J \implies ab \in J$ and $i \in I \implies i \in J$. That means that $1 \in J$ and consequently $J = R$

$\square$

def: Fractions equivalence relation

$$\begin{align*} &\sphericalangle \\ &\sim_F: (a, b) \sim_F (c, d) \iff ad = bc\\ \hline \\ &\sim_F - \text{fractions equivalence relation} \\ &\frac{a}{b} - \text{equivalence class} \end{align*}$$

def: Field of fractions

$$\begin{align*} &\sphericalangle \\ &B \in \mathcal R^{\mathcal {ID}} \\ & \mathfrak F(B) := (\{\frac{a}{b}, a, b \in B\}, +, \cdot )\\ &\frac{a}{b} + \frac{c}{d}:= \frac{ad + bc}{bd} \\ &\frac{a}{b} \cdot \frac{c}{d}:=\frac{ac}{bd} \\ \hline \\ &\mathfrak F(B) \text{ is a field of fractions over } B\\ \end{align*}$$

In other words, $\mathfrak F(B)$ is a collection of equivalence classes, as defined by the equivalence relation above. Conceptually, it can be seen as fractions represented by $a/b$, similar to the structure observed in rational numbers. Indeed, the field of rational numbers $\mathbb Q$, is an example of a field of fractions over the integers $\Z$.

Proposition 2.4.22: Field of fractions is a field

$$\begin{align*} &\sphericalangle \\ &B \in \mathcal R^{\mathcal {ID}} \\ \hline \\ &\mathfrak F(B) \in \mathcal F \end{align*}$$

Proof

First, let's prove that operations on $\mathfrak F(B)$ are well-defined. Assume $(a_1, b_1) \sim_F (a_2, b_2), (c_1, d_1) \sim_F (c_2, d_2)$, that is $a_1b_2 = a_2b_1, c_1d_2 = c_2d_1$

$$(a_1d_1+b_1c_1)(b_2d_2)=a_1d_1b_2d_2+b_1c_1b_2d_2=a_2d_1b_1d_2+b_1c_2b_2d_1= \\ =(a_2d_2+c_2b_2)b_1d_1 \implies (a_1d_1+b_1c_1, b_1d_1) \sim_F (a_2d_2+b_2c_2, b_2d_2)$$ $$a_1c_1b_2d_2=a_2 c_2b_1d_1 \implies (a_1c_1, b_1d_1) \sim_F (a_2c_2, b_2d_2)$$

It's easy to prove that operations $+$ and $\cdot$ are associative, commutative and distributive (this is essentially the same as proving it for $\mathbb Q$).

Let's check zero, identity and inverses. $0: = \frac{0}{1}, 1:=\frac{1}{1}, (\frac{a}{b})^{-1} = \frac{b}{a}$:

$$0+\frac{a}{b} = \frac{0}{1}+\frac{a}{b} = \frac{a\cdot 1 + 0 \cdot b}{ b \cdot 1}= \frac{a}{b} \\ \, \\ 1 \cdot \frac{a}{b} = \frac{1\cdot a}{ 1 \cdot b} = \frac{a}{b} \\ \, \\ \frac{a}{b}\cdot \frac{b}{a} = \frac{ab}{ab}=\frac{1}{1} =1$$

$\square$

Proposition 2.4.23: Field of fractions is a minimal field

$$\begin{align*} &\sphericalangle \\ &B \in \mathcal R^{\mathcal {ID}} \\ &E \in \mathcal F: B \subseteq_R E \\ \hline \\ &\exists\phi:\mathfrak F(B) \overset{1-1}{\rightsquigarrow}_R E: \forall a \in B: \phi(\frac{a}{1})=a \end{align*}$$

Proof

Define $\phi: \frac{a}{b} \mapsto ab^{-1}$. Let's prove, that the mapping is well-defined:

$$(a, b) \sim_F (c, d) \implies ad = bc \implies ab^{-1}=cd^{-1}$$

Next, let's prove that $\phi$ is a homomorphism:

$$\phi(\frac{a}{b} + \frac{c}{d})=\phi(\frac{ad+bc}{bd})=(ad+bc) \cdot (bd)^{-1}=\\ ab^{-1}+cd^{-1}=\phi(\frac{a}{b}) + \phi(\frac{c}{d}) \\ \phi(\frac{a}{b} \cdot \frac{c}{d}) = \phi(\frac{ac}{bd}) = ac(bd)^{-1} = ab^{-1}cd^{-1}=\phi(\frac{a}{b})\cdot\phi(\frac{c}{d})$$

Obviously $\phi(\frac{1}{1})=1$ so by $(2.4.20): \ker \phi = \{0\} \implies \phi:\mathfrak F(B) \overset{1-1}{\rightsquigarrow}_R E$

$\square$